삽입 정렬(Insertion Sort)
버블 정렬(Bubble Sort)의 비효율성을 개선하기 위해 등장한 정렬이다.
버블 정렬이 i번째와 i+1번째를 비교하며 위치를 바꿨다면
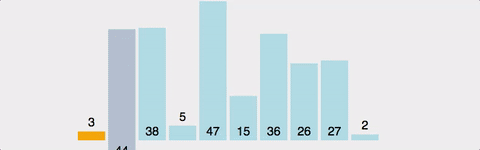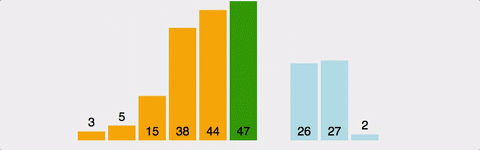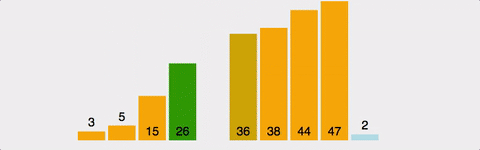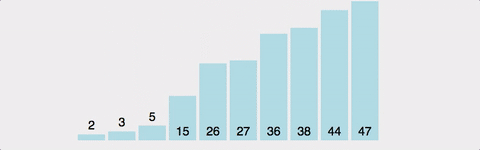
삽입 정렬은 배열을 정렬된 부분과 정렬되지 않은 부분으로 나누고, 정렬되지 않은 부분의 첫 번째 원소를 정렬된 부분과 비교한다.
그리고 자신보다 작은 값이 발견될 때, 그 위치에 삽입하는 방식의 정렬이다
삽입 정렬은 버블 정렬의 비교, 교환 횟수를 줄임으로써 효율이 높다
시간 복잡도
평균, 최악은 O(N^2) 이다
하지만 최선의 경우 O(N)의 시간 복잡도를 가진다
공간 복잡도
주어진 배열 외에 다른 공간이 필요 없으므로 O(N) 이다
특징
- 선택 정렬(Selection Sort), 버블 정렬과 같은 O(n^2) 알고리즘에 비해 상대적으로 빠르다
- 배열의 원소가 정렬되어 있을수록 속도가 좋다
- 제자리 정렬(Inplace algorithm)이다
- 안정 정렬(Stable Sort)이다
선택 정렬(Selection Sort)과 삽입 정렬
둘은 i번째 반복 후 i가 정렬된 순서로 온다는 점에서 유사하지만, 삽입 정렬이 더 효율적이다
선택 정렬은 i+1번째 요소를 찾기 위해 나머지 모든 요소를 탐색하지만,
삽입 정렬은 배치를 위해 필요한 만큼의 요소만 탐색하기 때문이다
코드
function insertionSort(arr) {
for(let i = 1; i < arr.length; i++) {
let cur = arr[i];
let left = i - 1;
while(left >= 0 && arr[left] > cur) {
arr[left + 1] = arr[left];
left--;
}
arr[left + 1] = cur;
}
return arr;
}
const arr = [5, 3, 7, 39, 28, 6, 1];
console.log(insertionSort(arr)); // [1, 3, 5, 6, 7, 28, 39]